그래프의 구조와 종류에 대한 설명입니다.
1. 그래프란?
노드(V, Vertex)와 그 노드를 연결하는 간선(E, Edge)을 하나로 모아 놓은 자료구조 이다.

즉, 연결되어 있는 객체 간의 관계를 표현할 수 있는 자료 구조이다.
생활 속의 예시,
지도, 지하철 노선도의 최단 경로, 전기 회로의 소자들, 도로(교차점과 일방 통행길), 선수 과목 등
2. 그래프의 종류
- 무방향 그래프(Undirected Graph)
무방향 그래프의 간선은 간선을 통해서 양 방향으로 갈 수 있다.
정점 A와 정점 B를 연결하는 간선은 (A, B)와 같이 정점의 쌍으로 표현한다.
(A, B)는 (B, A) 동일
Ex) 양방향 통행 도로

- 방향 그래프(Directed Graph)
간선에 방향성이 존재하는 그래프
A -> B로만 갈 수 있는 간선은 <A, B>로 표시한다.
<A, B>는 <B, A>는 다름
Ex) 일방 통행

- 가중치 그래프(Weighted Graph)
간선에 가중치가 주어진 그래프
Ex) 네비게이션 - 거리나 주행에 걸리는 시간 등으로 가중치를 줌 - 트리 그래프(Tree Graph)
순환을 갖지않는 연결 그래프
임의의 두 꼭짓점에 대하여, (v1, v2 ∈ V(T))
v1과 v2 사이의 경로의 수는 1 이하이다. - 밀집 그래프
간선의 수가 최대 간선의 수에 가까운 그래프 - 희소 그래프
간선이 얼마 없는 그래프
3. 그래프의 특징
- 그래프는 네트워크 모델 이다.
- 2개 이상의 경로가 가능하다.
즉, 노드들 사이에 무방향/방향에서 양방향 경로를 가질 수 있다. - self-loop 뿐 아니라 loop/circuit 모두 가능하다.
- 루트 노드라는 개념이 없다.
- 부모-자식 관계라는 개념이 없다.
- 간선의 유무는 그래프에 따라 다르다.
4. 연결과 강한 연결
- 연결 그래프(Connected Graph)
모든 두 꼭짓점사이에 경로가 존재하는 그래프이다. - 강한 연결 요소(Strongly Connected)
유향그래프에서 모든 정점이 모든 다른 정점에 대해 도달 가능한 경우를 말한다.

- 비연결 그래프(Disconnected Graph)
무방향 그래프에서 특정 정점쌍 사이에 경로가 존재하지 않는 경우
5. 그래프의 표현
그래프는 리스트와 행렬을 이용해 표현할 수 있다.
이때 인접 리스트와 인접 행렬을 활용하게 되는데,
- 인접이란?
: 그래프 (v,~)의 꼭짓점을 v의 원소이며,
u,v∈V에 대하여 u~v라면 u와 v가 인접한다고 한다.

1) 인접리스트
그래프의 한 꼭짓점에서 연결되어 있는 꼭짓점들을 하나의 연결리스트로 표현하는 방법이다.
- 장점: 메모리 효율이 높고 수정이 쉽다.
- 단점: 엣지를 확인할 때 모든 부분을 다 살펴봐야 확인할 수 있다.
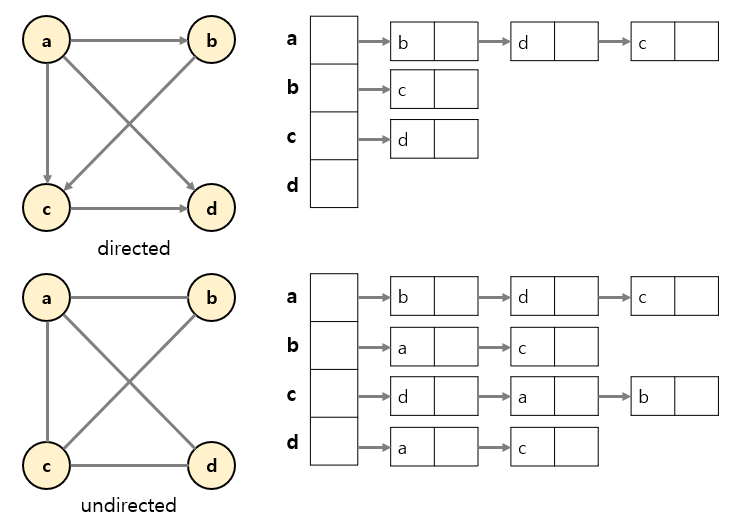
2) 인접 행렬
그래프에서 어느 꼭짓점들이 변으로 연결되었는지 나타내는 정사각 행렬로 표현하는 방법이다.
- 장점: 엣지의 유무확인이 간단하다.
- 단점: 공간이 v^2 만큼 필요하다.

'알고리즘 > 자료구조' 카테고리의 다른 글
| [자료구조] 트리 (Tree) (0) | 2020.01.22 |
|---|---|
| [자료구조] 스택과 큐 (0) | 2020.01.22 |
| [자료구조] 연결리스트 (0) | 2020.01.22 |
| [자료구조] 배열 (0) | 2020.01.22 |
| [자료구조] 자료구조란? (0) | 2020.01.22 |
